Batch 3 - Class 165 - Genetic Altruism
Pre-Class Exercise
Imagine folding a 8x8 chessboard into a mobius strip. Explore the paths of a bishop on the same (you may assume that the initial strip was printed back to back). You can rollover the edge of the strip when you encounter it.
Attendance Smiti, Muskaan, Liza, Anshi, Aashvi, Suryansh, Arjun, Anishka, Arnav
Class puzzles
"Let us suppose that you are standing on bank of a river, and a child is drowning. You can jump and save the child, but you have one in ten chance of drowning yourselves. Would you jump? What is the basis for such an action? Over millions of years, do we expect such behavior to strengthen or weaken?"
Let kids debate this out. See if they can get to the notion that they may save their close relatives but not someone unknown. Why is that? Is there a mathematical basis to doing so?
Now introduce the notion that suppose this instinct of jumping and saving a "close relative" is caused by a rare gene. Form a mathematical basis to survival and propagation of such a gene. Such a basis should exist towards maximizing the chances of such a gene propagating. i.e. relatedness of the other person x benefit to other person > reproductive cost to self.
Define "relatedness" - probability of another person carrying the same gene. For example, parents have a relatedness of 1/2. Siblings also have relatedness of 1/2 (1/4 from each parent). Cousins 1/8 (1/16 from each shared grandparent), and so on. In that sense, it is worth sacrificing yourselves to save two brothers, or eight cousins! Now one could argue that it also depends on reproductive benefits of saving those people versus own - for example, saving a child versus an old person. This is captured in "benefit".
- Let kids calculate relatedness of few relationships - cousins, second cousins, one shared grandparent, identical twins, etc.
- Let them work through an example to see how the gene will survive and propagate in the population with different behaviors. You are an animal who has found eight mushrooms. You can eat maximum of three, and get benefit of +6 from each. Or you could issue a "food call" and invite your brother, your cousin, and another random person (all at the same time), so that each of you get to eat 2 mushrooms each. Should you issue the food call?
- No food call, total benefit = 3x6=18. Food call, 2x6 + 2(1/2)x6+ 2(1/8)x6 + 0 = 19.5 - Hence the food call should be issued. Alternately, if there is a gene which issues a food call in this kind of circumstance, that gene is likely to multiply faster than the one which doesn't. Hence this behavior will be seen more and more in the successive populations.
Genetic altruism as an outcome of "selfish" behavior on part of the gene. Note that this selfish behavior is not intentional, but the right selfish behavior maximizes the chances of the gene multiplying and surviving. And hence that behavior persists, while others die off.
Cheating Genetic Behavior
Cuckoos lay eggs in nests of Song-birds. Song-birds are typically unable to recognize their own eggs, and will nurture cuckoo eggs. What kind of evolution do we expect to happen?
- Song-birds which can recognize their own eggs (or at least their own species' eggs) are likely to find favor in evolution
- Cuckoos who can product eggs that look more and more like Song-bird eggs are likely to find favor in evolution.
Relatedness in Honey bees
In case of honey bees, the queen mother has two sets of chromosomes, whereas the drone has only one set. The queen mates only once for her entire life. Thus each daughter born has complete set of chromosomes from her father, and half the set from her mother. Calculate the relatedness of a daughter with her mother, and with her sister
- 1/2 with mother, 3/4 with sister - note that this is higher than in human beings. Also the relatedness for a female, with own children is also 1/2
What could be the evolutionary impact of this?
- Females are motivated to help their mother produce and raise more sisters, than to go out and reproduce themselves
- Relatedness with brothers is only 1/4, so there is less "investment" in males, including killing of drones
- Promotes lifetime monogamy, because it then supports eusociality - i.e. sisters being motivated to nurture sisters rather than to reproduce.
Alarm Calls
In ground squirrels, alarm calls alert others to a danger, but also attract the predator to the animal issuing the alarm call. Alarm calls are seen to be most frequent when close relatives are nearby.
Other forms of Altruism
Altruism may arise for reasons other than genetic. For example, game theory also proposes "reciprocal altruism" as an outcome, with repeated occurances, and simple "tit-for-tat" strategy, starting with cooperation.
Homework Problem:
(Dudeney - 83) The four circles represent cycling paths. Four cyclists start at noon and cycle at speeds of six miles an hour, nine miles an hour, twelve miles an hour and fifteen miles an hour respectively. They agreed to ride until they all meet back at the center for the fourth time. The distance around each circle is one-third of a mile. When did they finish their ride.
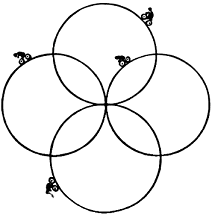
- Answer: 26 minutes 40 seconds past noon
References:
The Selfish Gene, by Richard Dawkins
536 Puzzles and Curious Problems, Henry Dudeney